NOTE: This is Part 3 of a three-part series demonstrating how we might model the card game War as a C# program. Part 1 is over here. You might want to use the sample project over on GitHub to follow along with this post. Also, check out my other posts in the Modeling Practice series!.
The Last Bit of Code
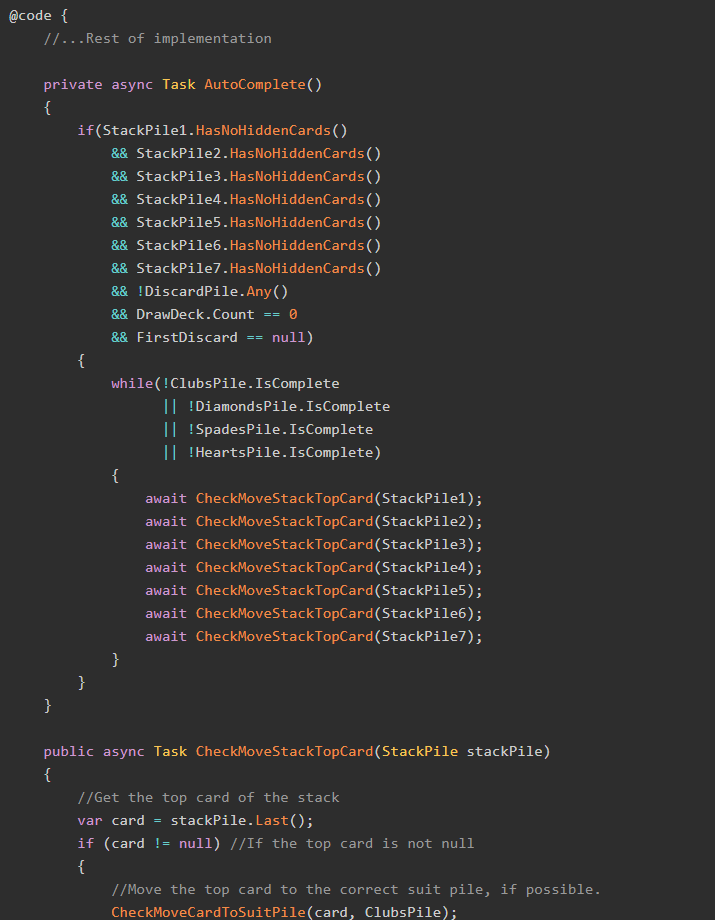
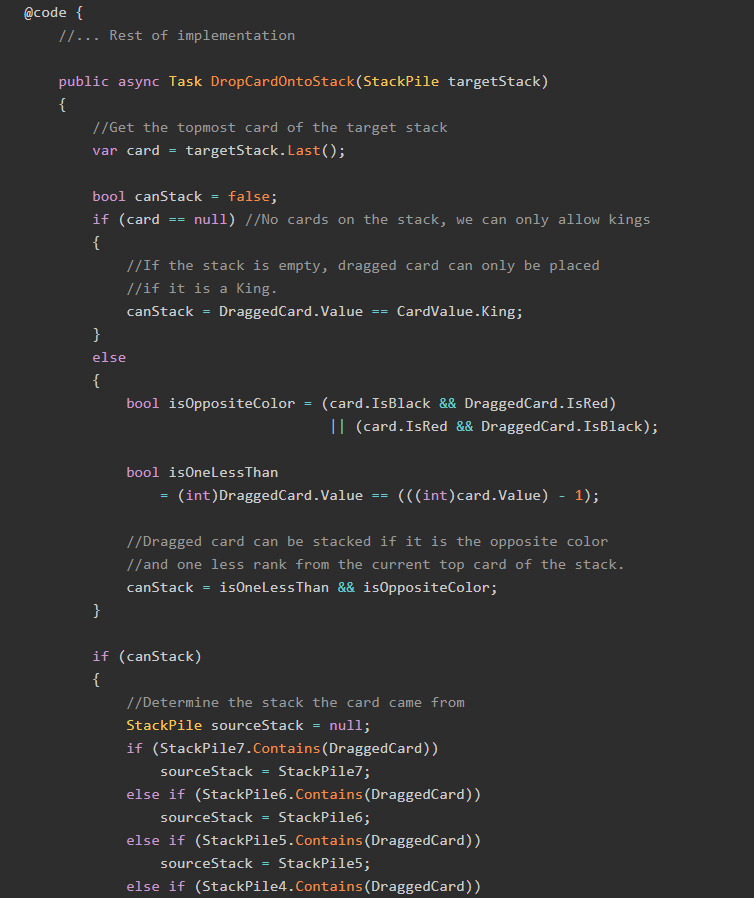
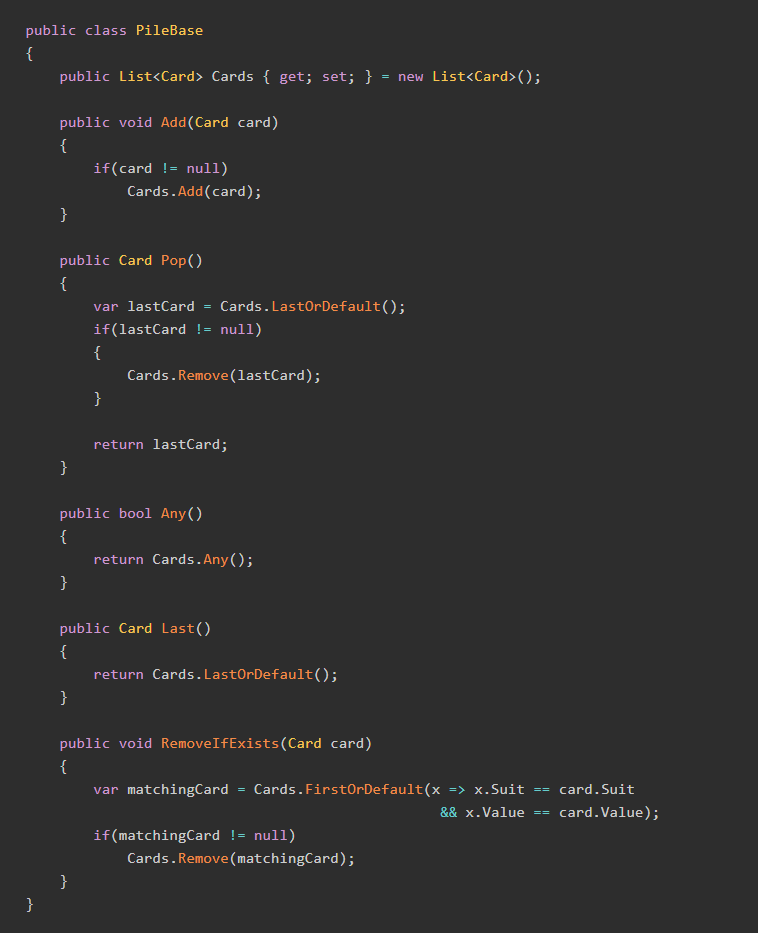
We have one last bit of code to write to make our program run: the all-important static void Main() method. Here's what we'll use to start.
class Program
{
static void Main(string[] args)
{
//Create game
Game game = new Game("Alice", "Bob");
while (!game.IsEndOfGame())
{
game.PlayTurn();
}
Console.Read();
}
}
NOTE: This code will fail in the case of an infinite game. We'll handle that problem a bit later.
Trial Runs
Now we can run the program to see if it works as intended. Let's do a sample run. Here's the last few lines of output from running the game once:
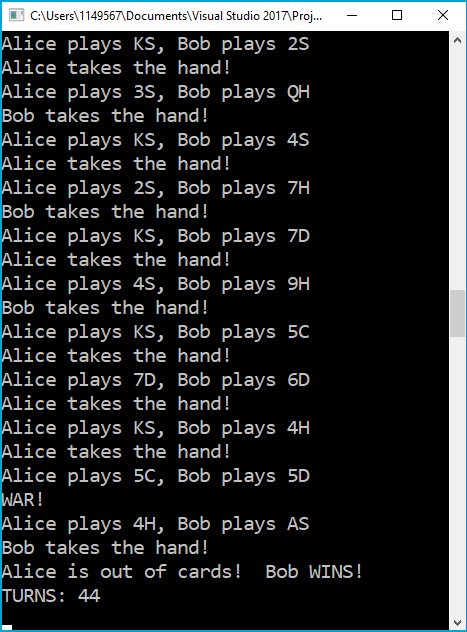
It looks as though in this game we ran into the situation where one of the players (Alice) ran out of cards during a WAR, and so immediately lost. That's good validation; it means that one of the decision points from the earlier posts works as intended.
But now... let's run it a thousand times. Oh, and let's also keep track of how many finite (e.g. finished) games there are, and the average number of turns each finite game takes. Here's the new Main() method:
class Program
{
static void Main(string[] args)
{
int totalTurnCount = 0;
int finiteGameCount = 0;
for (int i = 0; i < 1000; i++)
{
//Create game
Game game = new Game("Alice", "Bob");
while (!game.IsEndOfGame())
{
game.PlayTurn();
}
if (game.TurnCount < 1000)
{
totalTurnCount += game.TurnCount;
finiteGameCount++;
}
}
double avgTurn = (double)totalTurnCount / (double)finiteGameCount;
Console.WriteLine(finiteGameCount + " finite games with an average of " + Math.Round(avgTurn, 2) + " turns per game.");
Console.Read();
}
}
Here's the last few lines of output for this run:
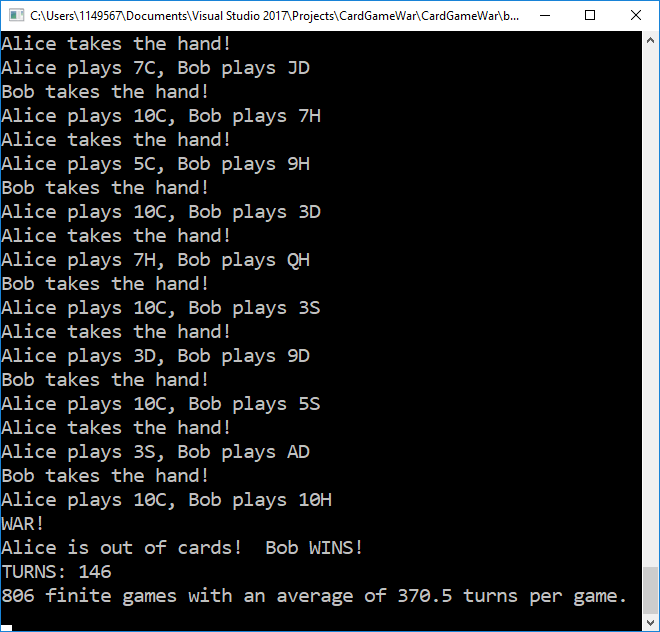
This kind of average is what I've seen a lot in running this app many times over. It's also the reason why I chose 1000 turns to be the cut-off point for an infinite game (thought I admit there is a small possibility that there could be games which would still resolve after 1000 turns, and this program will cut those out).
But we still want to find one more stat: do Bob and Alice win an equal number of games?
Who Wins the Most?
What we want to see now is if Alice or Bob wins statistically more games than the other. If one consistently wins more, we can assume that we introduced some kind of bias into our system.
To do this, we're going to make a change to the Game object from earlier, adding a new property called Winner:
public class Game
{
public Player Winner
{
get
{
if(!Player1.Deck.Any())
{
return Player2;
}
else if(!Player2.Deck.Any())
{
return Player1;
}
else
{
return null;
}
}
}
...
}
With this in place, we'll make a slight change to the Main() method to make it count the number of times each player wins, and display the difference to the console:
class Program
{
static void Main(string[] args)
{
int totalTurnCount = 0;
int finiteGameCount = 0;
string player1name = "Alice";
string player2name = "Bob";
int player1WinDifference = 0;
for (int i = 0; i < 1000; i++)
{
//Create game
Game game = new Game(player1name, player2name);
while (!game.IsEndOfGame())
{
game.PlayTurn();
}
if(game.Winner != null && game.Winner.Name == player1name)
{
player1WinDifference++;
}
else if(game.Winner != null && game.Winner.Name == player2name)
{
player1WinDifference--;
}
if (game.TurnCount < 1000)
{
totalTurnCount += game.TurnCount;
finiteGameCount++;
}
}
double avgTurn = (double)totalTurnCount / (double)finiteGameCount;
Console.WriteLine(finiteGameCount + " finite games with an average of " + Math.Round(avgTurn, 2) + " turns per game.");
if (player1WinDifference == 0)
{
Console.WriteLine("Both players won the same number of games!");
}
else if (player1WinDifference > 0)
{
Console.WriteLine(player1name + " won " + player1WinDifference.ToString() + " more games than " + player2name);
}
else
{
Console.WriteLine(player2name + " won " + (player1WinDifference * -1).ToString() + " more games than " + player1name);
}
Console.Read();
}
}
Let's run the app ten times to see if there's any bias in the system:
| Run | Big Winner | Differential | Average Turns | |
|---|---|---|---|---|
| 1 | Alice | 27 | 344.55 | |
| 2 | Alice | 20 | 296.79 | |
| 3 | Alice | 90 | 384.88 | |
| 4 | Alice | 6 | 320.44 | |
| 5 | Alice | 9 | 303.29 | |
| 6 | Alice | 20 | 346.17 | |
| 7 | Alice | 43 | 296.39 | |
| 8 | Alice | 125 | 249.9 | |
| 9 | Alice | 151 | 311.45 | |
| 10 | Alice | 63 | 316.91 |
That table speaks for itself. Alice won more games every damn time. That doesn't say BIAS so much as scream it.

Image is Bias, used under license
To be more certain, I ran the system another 20 times, and every time Alice won more games than Bob. Given a fairly-shuffled deck, I would expect Bob to be the bigger winner at least some of the time. Yet this is not happening.
This system is clearly biased. The question now becomes: why?
Summary
Our card-game WAR playing C# app is finished, and it works as intended... mostly. However, our system is biased somehow, in some way that's not easily seen. I intend to find out why.
Don't forget to check out the sample project on GitHub!. If you have any ideas as to why this system appears to be biased, I'd love to hear them. Sound off in the comments!
Happy Coding!