Anybody who's spent any time at a Windows machine in the last 26 years has probably played a few games of Minesweeper:

I mostly work in the ASP.NET space, and I'd been wondering for a few weeks how feasible it was to build a program that could solve Minesweeper automatically, similar to what I did for the board game Candy Land a few months ago. You can see where this is going: I wrote a Minesweeper solver program using C# and LINQ queries, and it runs (if I do say so myself) pretty darn well.
Being the motor mouth that I am, I can't possibly keep this to myself. We're going to build this solver together in this post. Let's build a Minesweeper solver with C# and LINQ!
NOTE: All code examples in this post have been edited for brevity, not completeness. If you want the full, working code, check out the repository on GitHub.
What Is Minesweeper?
Minesweeper is a popular single-person computer game which pits the player against a board full of panels. These panels can be clicked on to reveal what is underneath them. Some of these panels have mines on them, and the player loses the game if s/he reveals a mine. Any panel which does not have a mine on it instead has a number which tells the player how many of the adjacent panels (including diagonals) have mines on them. If the player clicks on a panel with 0 adjacent mines, the game reveals all the adjacent panels until a revealed panel has a number in it. The player may also "flag" panels so as to mark them as containing a mine.
From all this information, the player attempts to reveal the entire board EXCEPT those panels that have mines on them. Here's a completed board:

As you might imagine, the game gets more difficult the more densely the mines are laid out, which does not necessarily correspond to how large the board is. A huge board with only a few mines would be easy to solve, but a small board with a lot of mines is considerably more difficult.
Constructing the Game
Now that we understand the rules of the game, let's introduce some code to represent the game itself.
Panels
The smallest unit in the game are the squares that can be clicked on. I've taken to calling these "panels". In our C# project we have a class called Panel, which keeps track of its own coordinates on the board, what it contains, and its current state:
public class Panel
{
public int ID { get; set; }
public int X { get; set; }
public int Y { get; set; }
public bool IsMine { get; set; }
public int AdjacentMines { get; set; }
public bool IsRevealed { get; set; }
public bool IsFlagged { get; set; }
public Panel(int id, int x, int y)
{
...
}
}
There are three possible states for a panel:
- Hidden
- Flagged
- Revealed
The panel may contain either a mine or a count of the number of adjacent mines. X and Y represent the panel's horizontal and vertical coordinates within the board, respectively.
Once we have the Panel class, we can now build a class to represent the next game unit: the GameBoard.
GameBoard
The board need to keep track of a collection of panels. It must also track what the current status of the game is (e.g. whether the game is in progess, complete, or failed). Our GameBoard class looks like this:
public class GameBoard
{
public int Width { get; set; }
public int Height { get; set; }
public int MineCount { get; set; }
public List<Panel> Panels { get; set; }
public GameStatus Status { get; set; }
public GameBoard(int width, int height, int mines)
{
Width = width;
Height = height;
MineCount = mines;
Panels = new List<Panel>();
int id = 1;
for(int i = 1; i <= height; i++)
{
for (int j = 1; j <= width; j++)
{
Panels.Add(new Panel(id, j, i));
id++;
}
}
Status = GameStatus.InProgress; //Let's start the game!
}
}
public enum GameStatus
{
InProgress,
Failed,
Completed
}
We want to be able to create a GameBoard of any size, with any number of mines. The constructor of the GameBoard object creates a List<Panel> which represents all the panels on the board.
Now, wait a minute you might think, shouldn't the GameBoard also determine where the mines are placed? It turns out that doing so causes quite a bit of player frustration, so let's see if we can alleviate their pain by dynamically generating the mine placement after they select their first move.
The User's First Move
The most annoying thing about playing Minesweeper is when this happens:

It is entirely possible to lose the game in the first couple of moves, where the only valid strategy is to pick a panel at random. If the mines are placed randomly when the board is first created, then the user may accidentally reveal a mine on their first move. I wanted to eliminate this annoyance, and so this system doesn't actually place the mines on the board until after the user submits his first move.
In order to guarantee that the user's first move doesn't reveal a mine, and that s/he doesn't have to continue clicking randomly after the first move, I wanted an algorithm in which:
- The player's first move does not reveal a mine AND
- The player's first move reveals more than one panel.
In order to fit those rules within the game logic, the user's first move must always be to reveal a panel with 0 adjacent mines. There's a method in the GameBoard class called FirstMove() which implements this algorithm:
public void FirstMove(int x, int y, Random rand)
{
//For any board, take the user's first revealed panel + any neighbors of that panel to X depth, and mark them as unavailable for mine placement.
var depth = 0.125 * Width; //12.5% (1/8th) of the board width becomes the depth of unavailable panels
var neighbors = GetNeighbors(x, y, (int)depth); //Get all neighbors to specified depth
neighbors.Add(GetPanel(x, y)); //Don't place a mine in the user's first move!
//Select random panels from set of panels which are not excluded by the first-move rule
var mineList = Panels.Except(neighbors).OrderBy(user => rand.Next());
var mineSlots = mineList.Take(MineCount).ToList().Select(z => new { z.X, z.Y });
//Place the mines
foreach (var mineCoord in mineSlots)
{
Panels.Single(panel => panel.X == mineCoord.X && panel.Y == mineCoord.Y).IsMine = true;
}
//For every panel which is not a mine, determine and save the adjacent mines.
foreach (var openPanel in Panels.Where(panel => !panel.IsMine))
{
var nearbyPanels = GetNeighbors(openPanel.X, openPanel.Y);
openPanel.AdjacentMines = nearbyPanels.Count(z => z.IsMine);
}
}
This ensures that the first move will never reveal a mine, and will always reveal more than one panel. Consequently, the user is much more likely to engage with the game rather than just quitting out of frustration.
Finding the Neighbor Panels
One of the core functionalities that need to be provided by the GameBoard is that of finding the neighbor panels for a panel at specified coordinates. For example, take a look at this game:

The neighbors of that 3 panel are in all eight directions around the panel. So, we need a function which can find and return the neighbors of any given panel. Said function looks like this:
public List<Panel> GetNeighbors(int x, int y)
{
return GetNeighbors(x, y, 1);
}
public List<Panel> GetNeighbors(int x, int y, int depth)
{
var nearbyPanels = Panels.Where(panel => panel.X >= (x - depth) && panel.X <= (x + depth)
&& panel.Y >= (y - depth) && panel.Y <= (y + depth));
var currentPanel = Panels.Where(panel => panel.X == x && panel.Y == y);
return nearbyPanels.Except(currentPanel).ToList();
}
Why do we have the depth overload? Remember that the FirstMove() function requires us to mark a certain "depth" of panels from the user's first move as unavailable for mine placement.
Revealing a Panel
Now that we've got the code that creates the game board, we can start writing the code that allows the user to actually play that game. To start off, let's write a function in our GameBoard class which reveals a panel at a specified coordinate. Said function shall adhere to this methodology:
- Locate the specified panel and mark it as revealed.
- If the specified panel is a mine, end the game.
- If the specified panel has zero adjacent mines, reveal its neighbors in a cascade until numbered panels are revealed.
- Finally, check if the board is completed.
public void RevealPanel(int x, int y)
{
//Step 1: Find the Specified Panel
var selectedPanel = Panels.First(panel => panel.X == x && panel.Y == y);
selectedPanel.IsRevealed = true;
selectedPanel.IsFlagged = false; //Revealed panels cannot be flagged
//Step 2: If the panel is a mine, game over!
if (selectedPanel.IsMine) Status = GameStatus.Failed;
//Step 3: If the panel is a zero, cascade reveal neighbors
if (!selectedPanel.IsMine && selectedPanel.AdjacentMines == 0)
{
RevealZeros(x, y);
}
//Step 4: If this move caused the game to be complete, mark it as such
if (!selectedPanel.IsMine)
{
CompletionCheck();
}
}
We also need to implement the methods RevealZeros() and CompletionCheck() called in Steps 3 and 4 respectively.
Reveal Zeros
When a user clicks on a panel with no adjacent mines, we need to cascade through all of the adjoining panels and reveal every neighbor panel until the panels have a non-zero number in them. We can accomplish this using recursion:
public void RevealZeros(int x, int y)
{
var neighborPanels = GetNearbyPanels(x, y).Where(panel => !panel.IsRevealed);
foreach (var neighbor in neighborPanels)
{
neighbor.IsRevealed = true;
if (neighbor.AdjacentMines == 0)
{
RevealZeros(neighbor.X, neighbor.Y);
}
}
}
Completion Check
After revealing a panel, if that panel happened to be the last hidden panel which does not contain a mine, the game is complete. We can write this method using LINQ to exclude the mined panels from the hidden panels; if the two collections contain the same items, the game is complete. Here's our CompletionCheck method:
private void CompletionCheck()
{
var hiddenPanels = Panels.Where(x => !x.IsRevealed).Select(x => x.ID);
var minePanels = Panels.Where(x => x.IsMine).Select(x => x.ID);
if (!hiddenPanels.Except(minePanels).Any())
{
Status = GameStatus.Completed;
}
}
Flagging a Panel
The final piece of functionality we need to implement is flagging a panel. The user may flag any hidden panel, but the existence of a flag doesn't guarantee that that panel has a mine. Here's the method:
public void FlagPanel(int x, int y)
{
var panel = Panels.Where(z => z.X == x && z.Y == y).First();
if(!panel.IsRevealed)
{
panel.IsFlagged = true;
}
}
Challenges
There are two major challenges inherent in building a solver for Minesweeper, and they both deal with fundamental issues with the structure of the game itself.
Minesweeper is NP-Complete
We must first come to terms with the fact that no Minesweeper automated-solver will ever be able to solve all possible boards. This is because Minesweeper has been proven to be an NP-Complete problem, meaning that calculating a solution for all possible boards might be possible but would take an exorbitant amount of time.
Guessing Is (Eventually) Required
There are a great number of scenarios in Minesweeper that ultimately force the user to guess; that is, there is no way for the user to be absolutely certain of what panel to reveal next or where to place the next flag. Advanced solvers will use probability calculations to determine the most optimal next move whenever guessing is required; my solution does not do this. I am creating a solver to demonstrate the ideas needed, not to solve as many boards as possible.
With these two challenges in mind, let's list some goals that the solver needs to be able to fulfill.
Solving The Game
We want to build two kinds of solvers: a single-game solver and a multi-game solver. The multi-game solver will be used heavily in the analysis section of this post, and so is detailed there; this section will focus on the single-game variant.
The single-game solver should be able to:
- Start a game by randomly picking a panel.
- Use the strategies detailed below to reveal obvious panels and flag obvious mines.
- Allow the user to specify whether or not s/he wants the solver to use random guesses when a board becomes impossible to solve without guessing.
Game Solver Base Class
Let's start off by creating a class GameSolver, which will have properties and methods common to both the single-game and multi-game solvers.
public class GameSolver
{
protected int GetWidth() { ... }
protected int GetHeight() { ... }
protected int GetMines() { ... }
protected void WidthErrors(int width) { ... }
protected void HeightErrors(int height) { ... }
protected void MinesErrors(int mines) { ... }
}
The implementation of these methods is trivial; the source code for this file can be found in the GitHub repository.
Now we can start writing our single-game solver class.
Single-Game Solver
Here's the skeleton for the single-game solver; the rest of this post will be about filling in the functionality.
public class SingleGameSolver : GameSolver
{
public GameBoard Board { get; set; }
public Random Random { get; set; }
public SingleGameSolver(Random rand)
{
Random = rand;
int height = 0, width = 0, mines = 0;
while (width <= 0)
{
width = GetWidth();
WidthErrors(width);
}
while (height <= 0)
{
height = GetHeight();
HeightErrors(height);
}
while (mines <= 0)
{
mines = GetMines();
MinesErrors(mines);
}
Board = new GameBoard(width, height, mines);
}
public SingleGameSolver(GameBoard board, Random rand)
{
Board = board;
Random = rand;
}
}
Random Number Generation
A big part of creating the Minesweeper board is the use of a random-number generator; in this case, that generator is the Random class. However, Random is not a true random-number generator (rather being psuedo-random), so when I was coding up this project I started noticing that a lot of the boards had the same mine placement, the same first move, etc.
Turns out that Random uses the current clock ticks as a seed, and so by creating a new Random class over and over again in quick succession, I would get the same "random" numbers many times in a row. Consequently, my solution passes a single instance of Random around to where it is needed, and therefore we won't see duplicate boards or duplicate move sets when running many games in a row (as we will do in the Analysis section).
Strategies
When attempting to solve a Minesweeper board, there are many simple strategies the player can use to up the odds of their winning the game. The four strategies below were the easiest to code for and can solve a great number of easy-to-intermediate boards.
Obvious Mines
Look at this game board:
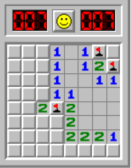
I know from looking at the board that the three panels with flags on them must be mines. How do I know this? Because for each of those panels, there is an adjacent "1" panel that has no other hidden panels around it.
In general, this strategy is summed up as: "For any number panel, if the number of hidden adjacent panels equals the number in the current panel, all the adjacent hidden panels must be mines."
In our SingleGameSolver class, we write that as the following method:
public void FlagObviousMines()
{
var numberPanels = Board.Panels.Where(x => x.IsRevealed && x.AdjacentMines > 0);
foreach(var panel in numberPanels)
{
//For each revealed number panel on the board, get its neighbors.
var neighborPanels = Board.GetNeighbors(panel.X, panel.Y);
//If the total number of hidden == the number of mines revealed by this panel...
if(neighborPanels.Count(x=>!x.IsRevealed) == panel.AdjacentMines)
{
//All those hidden panels must be mines, so flag them.
foreach(var neighbor in neighborPanels.Where(x=>!x.IsRevealed))
{
Board.FlagPanel(neighbor.X, neighbor.Y);
}
}
}
}
With the obvious mines flagged, can we determine the inverse? Can we determine, for a single panel, whether or not all the hidden neighbors are not mines? We sure can.
Obvious Number Panels
Here's another sample game in progress:

See the 2 panel whose neighbors I've highlighted? Notice that, due to other panels, we've been able to flag two of that panel's neighbors as having mines. Consequently, any remaining hidden panels must not have mines:

In general, the logic for this strategy goes like this: for any given revealed number panel, if the number of flags adjacent to that panel equals the number in the panel, then all hidden adjacent unflagged panels cannot be mines.
public void ObviousNumbers()
{
var numberedPanels = Board.Panels.Where(x => x.IsRevealed && x.AdjacentMines > 0);
foreach(var numberPanel in numberedPanels)
{
//Foreach number panel
var neighborPanels = Board.GetNeighbors(numberPanel.X, numberPanel.Y);
//Get all of that panel's flagged neighbors
var flaggedNeighbors = neighborPanels.Where(x => x.IsFlagged);
//If the number of flagged neighbors equals the number in the current panel...
if(flaggedNeighbors.Count() == numberPanel.AdjacentMines)
{
//All hidden neighbors must *not* have mines in them, so reveal them.
foreach(var hiddenPanel in neighborPanels.Where(x=>!x.IsRevealed && !x.IsFlagged))
{
Board.RevealPanel(hiddenPanel.X, hiddenPanel.Y);
}
}
}
}
Using just these two strategies, we can solve a lot of simple boards. But there's one other simple strategy I chose to implement: an endgame check for the number of remaining mines.
Endgame Flag Count
Near the end of the game, there's a simple way that we can determine whether or not we've solved the board. Check out this board:

On a beginner board, there are 10 mines; on this board, we have flagged 10 mines. Therefore all the remaining panels must not have mines:
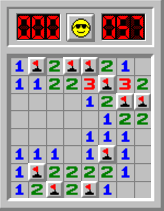
The endgame strategy, in short, is that if the number of flagged panels equals the number of mines on the board, all the remaining panels cannot have mines. Therefore we can reveal all of those panels:
public void Endgame()
{
//Count all the flagged panels. If the number of flagged panels == the number of mines on the board, reveal all non-flagged panels.
var flaggedPanels = Board.Panels.Where(x => x.IsFlagged).Count();
if(flaggedPanels == Board.MineCount)
{
//Reveal all unrevealed, unflagged panels
var unrevealedPanels = Board.Panels.Where(x => !x.IsFlagged && !x.IsRevealed);
foreach(var panel in unrevealedPanels)
{
Board.RevealPanel(panel.X, panel.Y);
}
}
}
These three strategies comprise the portion of the solver that can actually solve the board. However, there's one more "strategy" (and I use the term loosely) that we need to implement.
Random Guessing
It's entirely possible (probable even, especially on harder boards) that at some point we will have to randomly reveal a panel in order to proceed with solving the board. Here's our function to do so:
public void RandomMove()
{
var randomID = Random.Next(1, Board.Panels.Count);
var panel = Board.Panels.First(x => x.ID == randomID);
while(panel.IsRevealed || panel.IsFlagged)
{
//We can only reveal an hidden, unflagged panel
randomID = Random.Next(1, Board.Panels.Count);
panel = Board.Panels.First(x => x.ID == randomID);
}
Board.RevealPanel(panel.X, panel.Y);
}
With these four strategies in place, there's only one more question we need to answer: how do we know if there are still possible moves we can make without guessing?
Checking For Available Moves
One additional feature of this solver is that it needs to check if there are available moves; if there are no available moves we must guess randomly. The Obvious Mines and Endgame strategies can be run at any time without fear of failing the game (since they only flag panels, they don't reveal them), therefore the only strategy we need to check is the Obvious Number Panels strategy. Here's the function for that:
public bool HasAvailableMoves()
{
var numberedPanels = Board.Panels.Where(x => x.IsRevealed && x.AdjacentMines > 0);
foreach (var numberPanel in numberedPanels)
{
//Foreach number panel
var neighborPanels = Board.GetNeighbors(numberPanel.X, numberPanel.Y);
//Get all of that panel's flagged neighbors
var flaggedNeighbors = neighborPanels.Where(x => x.IsFlagged);
//If the number of flagged neighbors equals the number in the current panel...
if (flaggedNeighbors.Count() == numberPanel.AdjacentMines)
{
return true;
}
}
return false;
}
(Yes, I know this could be optimized, it's a lot of repeated code, etc. It's an example, not production code.)
Order of Operations
Now that we've got the four strategies coded up, let's determine in what order they should fire. Generally speaking, we need to flag mines first before revealing new panels so that the flagged panels are not able to be revealed. Here's the order of operations for the single game solver:
- While the game is not solved or failed
- If zero panels have been revealed, submit user's first move.
- Flag the obvious mines.
- Check for available "Obvious Number Panel" moves.
- Reveal the obvious number panels.
- Check for the endgame mine count situation.
- If there are no available moves, randomly reveal a panel.
In other words:
public BoardStats Solve()
{
//Step 1
while (Board.Status == GameStatus.InProgress)
{
if (!Board.Panels.Any(x=>x.IsRevealed))
{
//Step 2
FirstMove();
}
//Step 3
FlagObviousMines();
//Step 4
if (HasAvailableMoves())
{
//Step 5
ObviousNumbers();
}
else //No available moves, we must guess to continue
{
//Step 7
RandomMove();
}
//Step 6
Endgame();
}
//Display messages
}
Analysis
Now that we've got the game itself coded up and a single-game solver working, let's combine many game solvers to analyze how well our strategies perform on different kinds of boards. To do this, we must first create the Multi-Game Solver we mentioned earlier.
Multi-Game Solver
Before we can start solving (or at least attempting to solve) lots of Minesweeper games, we must first create a multi-game solver. The multi-game solver needs to know the following properties of the game:
- The dimensions of the boards
- How many mines exist on each board
- How many boards to solve
The MultiGameSolver class in our solution looks like this:
public class MultiGameSolver : GameSolver
{
public int BoardWidth { get; set; }
public int BoardHeight { get; set; }
public int MinesCount { get; set; }
public int BoardsCount { get; set; }
public int GamesCompleted { get; set; }
public int GamesFailed { get; set; }
public MultiGameSolver()
{
//Get height, width, mines count, number of boards
}
public void Run()
{
Random rand = new Random();
List<BoardStats> stats = new List<BoardStats>();
Console.WriteLine("Solving Games...");
for(int i = 0; i < BoardsCount; i++)
{
GameBoard board = new GameBoard(BoardWidth, BoardHeight, MinesCount);
SingleGameSolver solver = new SingleGameSolver(board, rand);
var boardStats = solver.Solve();
stats.Add(boardStats);
if(solver.Board.Status == Enums.GameStatus.Completed)
{
GamesCompleted++;
}
else if(solver.Board.Status == Enums.GameStatus.Failed)
{
GamesFailed++;
}
}
Console.WriteLine("Games Completed: " + GamesCompleted.ToString());
Console.WriteLine("Games Failed: " + GamesFailed.ToString());
//Calculate and display stats
}
}
We also have the BoardStats class called out above:
public class BoardStats
{
public double TotalPanels { get; set; }
public double PanelsRevealed { get; set; }
public double Mines { get; set; }
public double FlaggedPanels { get; set; }
public double PercentMinesFlagged { get; set; }
public double PercentPanelsRevealed { get; set; }
}
With the Multi-Game Solver written, we can now start to get statistics for each board type, beginning with the Beginner boards.
Beginner Boards
First, let's take a look what a beginner board looks like. Here's a sample beginner board:
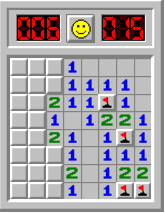
The dimensions of a beginner board are 9 panels by 9 panels, with 10 randomly-placed mines. This gives us a board density of 12.3%. These kinds of boards should be relatively easy to solve.
We're going to run five groups of 100 boards each, and analyze the number of boards solved and failed, as well as the number of mines flagged and panels revealed. Here's the data for these runs:
| Run # | Games Solved | Games Failed | % Mines Flagged | % Panels Revealed |
|---|---|---|---|---|
| 1 | 83 | 17 | 90.1% | 95.54% |
| 2 | 85 | 15 | 90.4% | 95.68% |
| 3 | 82 | 18 | 90.8% | 95.64% |
| 4 | 80 | 20 | 90.3% | 95.27% |
| 5 | 77 | 23 | 87.4% | 93.7% |
On average, we're solving about 80%-82% of the boards, with 88%-89% of the mines correctly flagged and 95% of the panels revealed. That's pretty darn good if I do say so myself.
Let's ramp up the difficulty a bit and see how well the solver holds up.
Intermediate Boards
In Minesweeper, intermediate boards look like this:
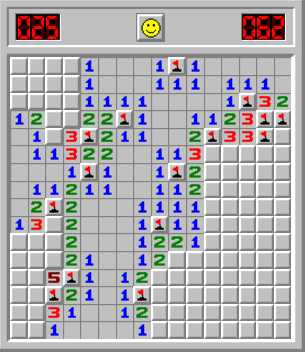
This time the board is 16x16 with 40 mines, given a board density of 15.6%. Let's run the same set of tests (5 runs of 100 boards each) and see how well the solver does this time.
| Run # | Games Solved | Games Failed | % Mines Flagged | % Panels Revealed |
|---|---|---|---|---|
| 1 | 49 | 51 | 86.82% | 90.93% |
| 2 | 41 | 59 | 83.75% | 89.63% |
| 3 | 45 | 55 | 83.58% | 89.3% |
| 4 | 39 | 61 | 82.88% | 89.12% |
| 5 | 44 | 56 | 84.4% | 89.27% |
This is where the results get interesting. We didn't solve more than half the intermediate boards on any run, so by that metric the solver's not doing so hot. But we still flagged approx 84% of the mines and revealed approx 89% of the panels, so we're getting a lot done before we fail the boards. What this tells me is that once the solver solves a large percentage of the board, it has to start guessing, and that's where it begins to fail.
Let's see if the this is born out by the expert level boards.
Expert Boards
Once again, here's an expert board for reference.

This time the board is 30 panels wide and 16 panels tall with a whopping 99 mines! That gives us a board density of 20.6%, the highest we've seen so far (after all, this is expert mode). With the high density, we should expect that we'll solve even less games than we did on the intermediate boards. Here's the data:
| Run # | Games Solved | Games Failed | % Mines Flagged | % Panels Revealed |
|---|---|---|---|---|
| 1 | 0 | 100 | 47.49% | 58.59% |
| 2 | 2 | 98 | 45.89% | 56.57% |
| 3 | 0 | 100 | 45.56% | 56.17% |
| 4 | 0 | 100 | 44.18% | 54.86% |
| 5 | 0 | 100 | 45.36% | 55.29% |
Well. I don't think the results could be any clearer than that. We solved 2 games out of a possible 500, so yeah, the solver's not going to get very far on these expert boards.
On the other hand, it did flag about 45% of the mines and revealed 56% of the number panels, so the solver's still making progress. It's just that with the much higher mine density, eventually the solver's going to have to make a guess, and eventually it's going to guess wrong. At this point, the simple strategies we've implemented for this solver won't help us very much except to get us started.
Summary
Our solver uses four strategies to solve Minesweeper boards:
- Check for obvious mines
- Check for obvious number panels
- Check for "endgame" all mines flagged situation
- If none of the above are available, randomly guess a panel
This solver, while not able to solve all boards, can complete a large percentage of them. It turns out that the solver does pretty darn well at the beginner boards and fairly well on the intermediate boards, but fails miserably once we get to the expert level. To be fair, that's kinda what we expected; we're not using any terribly advanced methodology here, just simple Minesweeper strategy. The fact that said strategies solve any number of the boards is amazing, frankly.
Don't forget to check out the repository for this project!
Let me know what you thought of this post: was it too deep, too shallow, too much, too little? I'd love to hear any feedback you have in the comments!
Happy Coding!








