Modeling Practice
Stories about modeling real-world problems, such as board games like UNO and Battleship, with code.
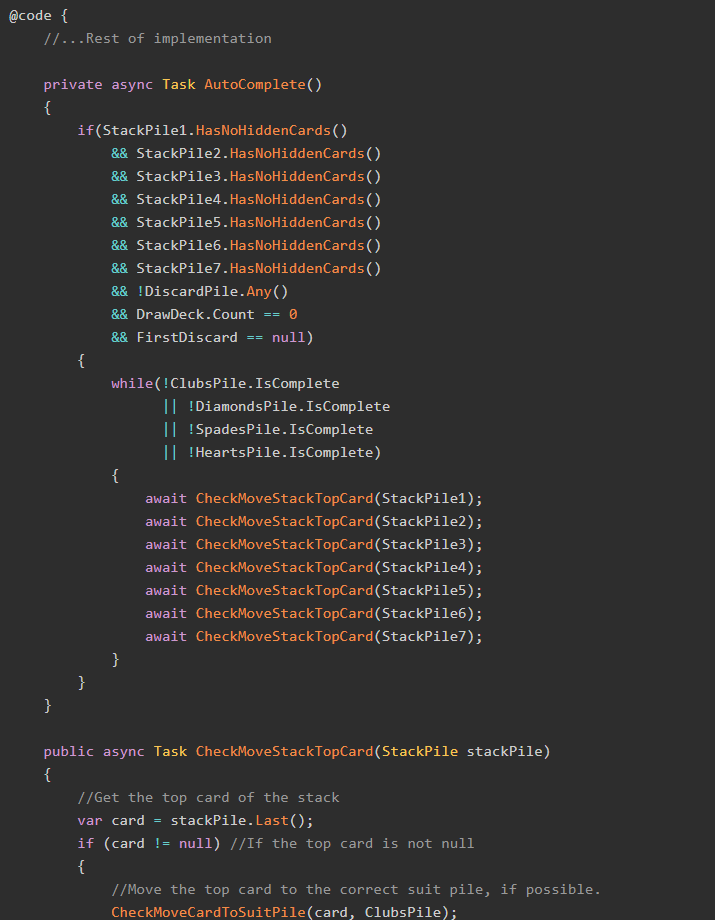
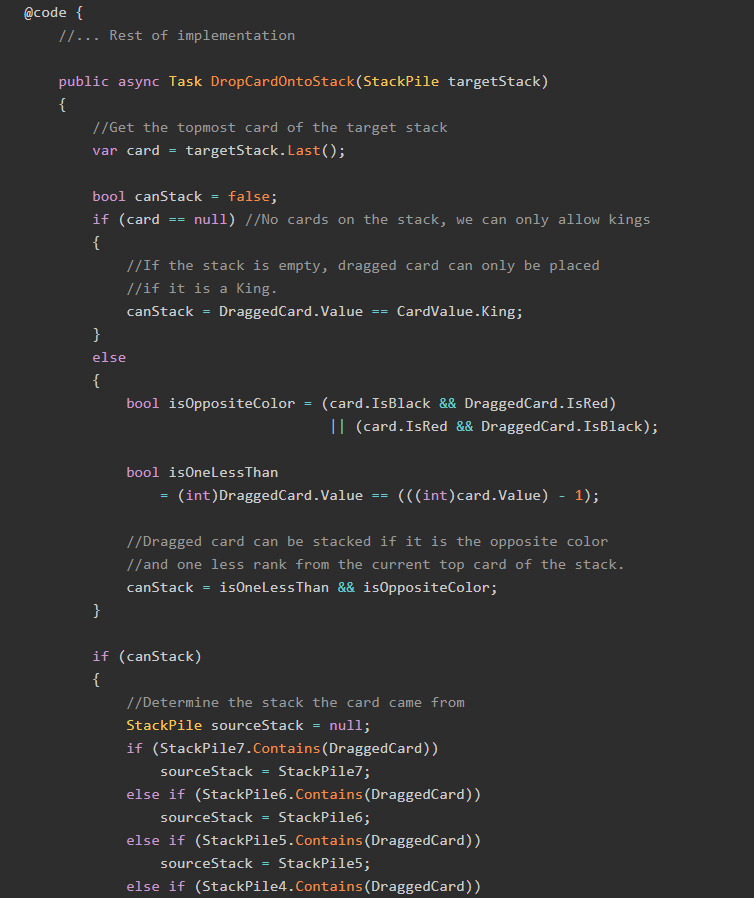
Let's finish our Solitaire in Blazor and C# implementation by adding two nice-to-have features!
Let's implement drag-and-drop and build a working game of Solitaire!
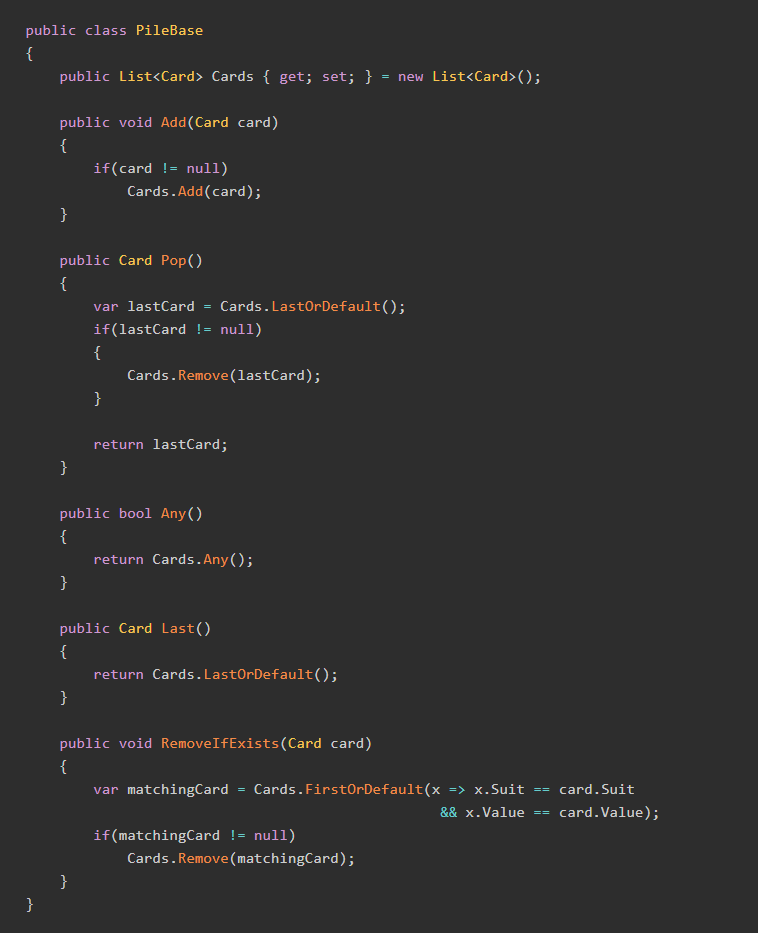
We need classes for a Card, the DrawPile, the DiscardPile, SuitPiles, and the Stacks.
The biggest time waster in history, now in C# and Blazor WebAssembly!
All that's left to do is implement scoring, levels, music, the grace period, a new game button, and a previous high score cookie.
Let's implement more major features, like keyboard controls, grid focus, clearing rows, and more!
Let's write up Blazor components to show the game grid, and write a game loop to make the tetrominos fall!
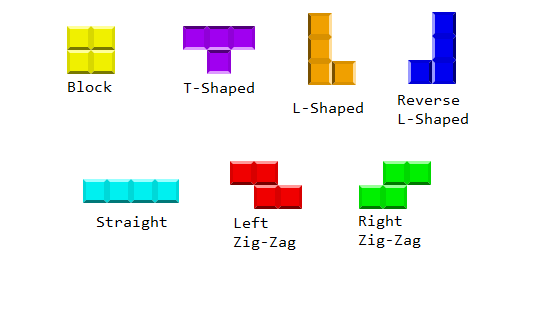
Four parts each, in different layouts. Let's build them all!
C#, .NET, Web Tech, The Catch Block, Blazor, MVC, and more!
You've successfully subscribed to Exception Not Found
Welcome back! You've successfully signed in.
Great! You've successfully signed up.
Your link has expired
Success! Your account is fully activated, you now have access to all content.