Note: This post is the first in a three-part series based around modeling the card game UNO in a C# application. You may want to use the GitHub repository to follow along.
I often find that one of the hardest things to do in software development is take a large complex problem and break it down into smaller, more easy problems. As with nearly anything, the only way to get better at this is to practice, so today I'm introducing a new series that aims at providing a practice for both and my readers on how to take real-world problems and model them in C# applications. I'm calling them Modeling Practice.
I've written two groups of posts prior to this one that can be also be considered modeling practice. The first one was a series based around the board game Candy Land, and the second was my longest post ever which detailed how to solve many games of Minesweeper. But for this series of posts, I've decided to take on my hardest challenge yet.
In this series, we're going to model the Mattel card game UNO.

I have very fond memories of this game; my family played it quite a bit when I was younger, and now playing a hand of it is one of my son's favorite things to do. However, this game is considerably more complex than either Candy Land (in which, after the cards are dealt, the winner has already been determined) or Minesweeper (which can be solved mathematically, in many cases). The problem here is that when playing UNO there is some strategy involved; part of designing this model will be making proper and careful assumptions about how these
Let's see if we can take this large problem (how can we play UNO in a C# application?) and break it down into smaller components, then actually build those components to produce a working application. (Hint: we absolutely can, and the repository for it is over on GitHub).
Assumptions and Goals
In this series, we will model the playing of a single UNO round, from the dealing of cards, to the play of the round, to the players shouting "Uno!", to assigning a score to each player at the end of the hand. What we're trying to do here is practice taking a real-world scenario and breaking it down into manageable pieces so that we can solve for those pieces individually, rather than trying to tackle the entire problem at the same time.
We will have to make some assumptions: for example, our players will never forget to yell "Uno!". But our goal is not to model every single possibility; our goal is to make some sacrifices to the demands of the real world and model a working solution to the problem at hand. We will phrase the problm like this:
How would you model a round of UNO being played?
To do that, we must first make sure we understand the rules of the game.
How To Play UNO
For those of you who might not be familiar with the game UNO, let's describe how we play a round. Those of you who do know how to play can skip to the next section.
Basic Rules
Uno! is a card game in which players attempt to remove all cards from their hands by discarding them. Each player starts the round with 7 random cards in their hand.
During a player's turn, s/he attempts to discard a card by matching it to the last-discarded card, either by playing a card with the same color, the same face value, or by playing a wild card.
When a player has one card remaining in their hand, they must shout "Uno!" If they fail to do so, and another player notices and calls them out on it, the player must draw two cards (or one, rules vary).
The Deck
The card deck in Uno is comprised of 108 cards: 25 of each color (red, green, blue, yellow) and 8 wild cards. The color cards each have a corresponding value of 0-9 or an "action" card. Action cards can do the following:
- Skip (🚫): Skips the next player's turn.
- Reverse (⇆): Reverses the turn order.
- Draw Two (+2): Forces the next player to draw two cards and miss their turn.
The wild cards also come in two flavors:
- Wild: Allows the player to declare which color the next card should be.
- Wild Draw Four (+4): Allows the player to declare which color the next card should be AND forces the next player to draw four cards and miss their turn. This card can only be played if no other card in the player's hand can be played.
Here's a sample deck of UNO cards:
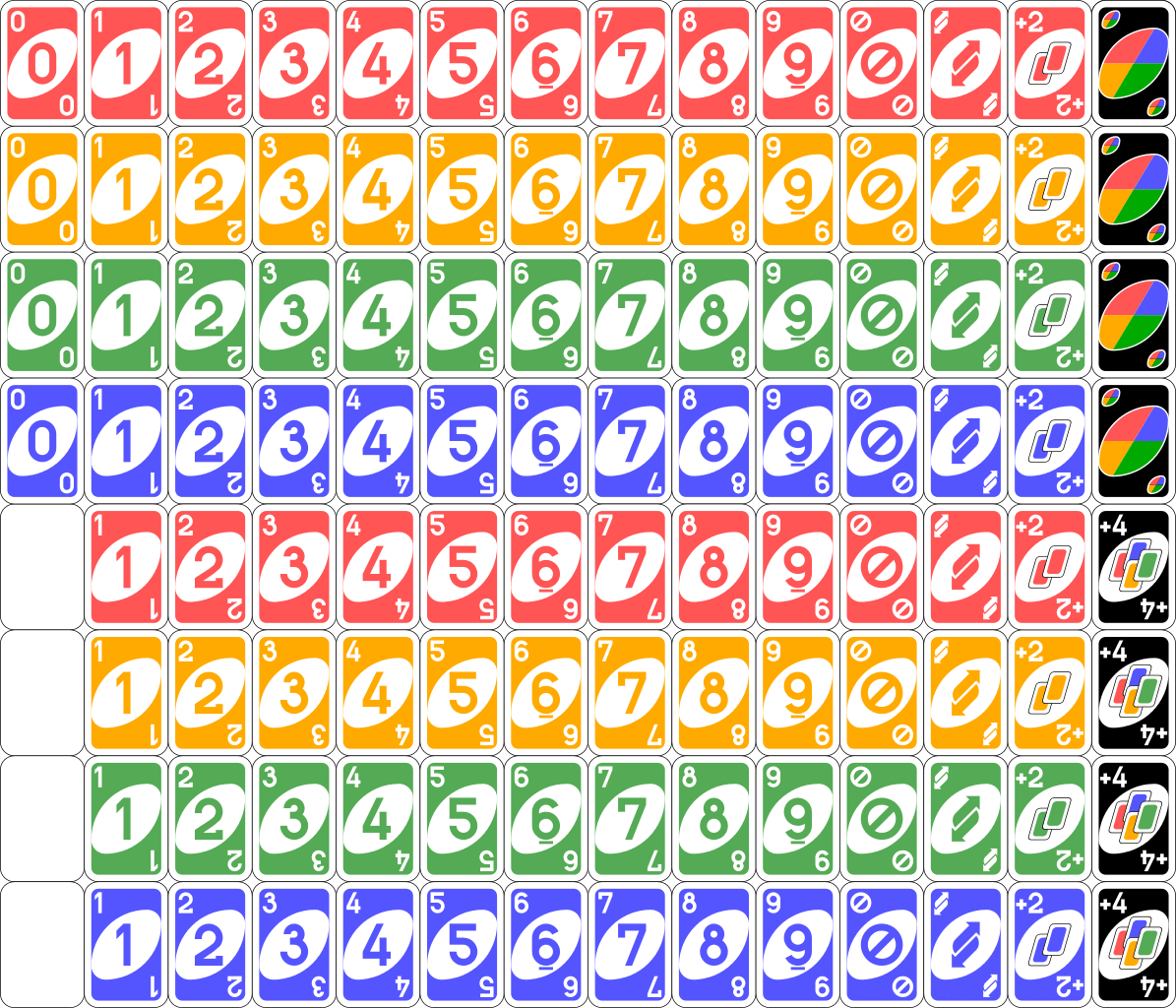
Scoring
In a real UNO game, players are assigned a score depending on how many cards are left in their hand and the values of those cards. The cards are worth the following points:
- 0-9: What number is shown.
- Draw Two, Reverse, Skip: 20 points.
- Wild, Wild Draw Four: 50 points.
The original Mattel rules state that as players reach a 500 point threshold, those players are eliminated and play continues with the remaining players. The version my family played, however, had the entire game stop when a person reached 500 points, and the person with the lowest number of points would win.
Official Rules
The official rules are a pain to find on Mattel's site, so here's a link directly to the version we'll be using. Please note that different versions of UNO occasionally use different rules as well.
Breaking Down The Problem
Now that we know the rules of the game, we can start to break our big problem down into little ones.
Let's think about this: if we wanted to play UNO in real life but had never actually played it before, what would we need? I see five different things we would need:
- Cards: We need the physical cards to play the game.
- Game Setup: How do we shuffle and deal the cards at the beginning of the game?
- Players: How many players will play the game? Since we're not playing with real people, how will our fake players behave during the game?
- Game End: How will we know when the game is over?
- Scoring: How do we know who won?
We'll model each of these independently, starting with the cards. The game setup and the players will be modeled in Part 2 of this series, and the game end scenarios and scoring will be modeled in Part 3.
First Step: Modelling the Cards
Obviously we cannot play a game of UNO without the cards, so let's tackle the medium-sized problem of modelling the cards themselves.
Here's a sample UNO card:

Each card has three properties:
- A color
- A value
- A score
For our sample card, it's pretty clear that the color is Green, the value is 0, and the score is 0. For each of the numbered cards, the value equals the score, but for the action and wild cards, the score and value are different.
Let's model the possible colors and values using enumerations:
public enum CardColor
{
Red,
Blue,
Yellow,
Green,
Wild
}
public enum CardValue
{
Zero,
One,
Two,
Three,
Four,
Five,
Six,
Seven,
Eight,
Nine,
Reverse,
Skip,
DrawTwo,
DrawFour,
Wild
}
With the range of possible colors and values defined, we can build a simple class to represent a single card:
public class Card
{
public CardColor Color { get; set; }
public CardValue Value { get; set; }
public int Score { get; set; }
}
With that, we have modeled the cards themselves. Now we can begin modeling how to set up a hand of UNO.
Setting Up The Game
Here's a (totally not staged) shot of an UNO game which has been set up for four players:

(Yes, we play on the floor. It's easier for little hands to reach the draw pile than sitting at the table would be.)
There are four hands of seven cards each, one for each player, as well as a draw pile and a discard pile. Let' use my l33t paint skillz to show which is which.

In a real game, it's up the players to enforce the rules and make sure everyone plays by them. But in our model, we'll need an object to do that, and we will call this object the GameManager.
public class GameManager
{
public List<Player> Players { get; set; }
public CardDeck DrawPile { get; set; }
public List<Card> DiscardPile { get; set; }
}
We will define what the Player class is during the Strategy section, so for now let's focus on the properties DiscardPile and DrawPile.
DiscardPile is just a List<Card>, and really only exists so that we a) know what card was last discarded and b) can reshuffle the discard pile into the draw pile when the draw pile runs out of cards.
DrawPile is the more interesting property. In my model, it is a class CardDeck, which looks something like this:
public class CardDeck
{
public List<Card> Cards { get; set; }
public CardDeck() { ... }
public void Shuffle() { ... }
public List<Card> Draw(int count) { ... }
}
Let's take each of the three methods in this class and define what we need them to do.
Creating the Cards
When the CardDeck is created, we need it to populate itself with enough cards to represent a proper UNO deck. To do this, we use the constructor to create enough cards.
Here's the full constructor, with annotated comments.
public CardDeck()
{
Cards = new List<Card>();
//For every color we have defined
foreach (CardColor color in Enum.GetValues(typeof(CardColor)))
{
if (color != CardColor.Wild) //Wild cards don't have a color
{
foreach (CardValue val in Enum.GetValues(typeof(CardValue)))
{
switch (val)
{
case CardValue.One:
case CardValue.Two:
case CardValue.Three:
case CardValue.Four:
case CardValue.Five:
case CardValue.Six:
case CardValue.Seven:
case CardValue.Eight:
case CardValue.Nine:
//Add two copies of each color card 1-9
Cards.Add(new Card()
{
Color = color,
Value = val,
Score = (int)val
});
Cards.Add(new Card()
{
Color = color,
Value = val,
Score = (int)val
});
break;
case CardValue.Skip:
case CardValue.Reverse:
case CardValue.DrawTwo:
//Add two copies per color of Skip, Reverse, and Draw Two
Cards.Add(new Card()
{
Color = color,
Value = val,
Score = 20
});
Cards.Add(new Card()
{
Color = color,
Value = val,
Score = 20
});
break;
case CardValue.Zero:
//Add one copy per color for 0
Cards.Add(new Card()
{
Color = color,
Value = val,
Score = 0
});
break;
}
}
}
else //Handle wild cards here
{
//Add four regular wild cards
for (int i = 1; i <= 4; i++)
{
Cards.Add(new Card()
{
Color = color,
Value = CardValue.Wild,
Score = 50
});
}
//Add four Draw Four Wild cards
for (int i = 1; i <= 4; i++)
{
Cards.Add(new Card()
{
Color = color,
Value = CardValue.DrawFour,
Score = 50
});
}
}
}
}
That method is pretty straightforward, and results in us having a complete deck of UNO cards. But, something's missing. Obviously we wouldn't want to play the game without shuffling the cards first, so let's implement that Shuffle() method:
public void Shuffle()
{
Random r = new Random();
List<Card> cards = Cards;
for (int n = cards.Count - 1; n > 0; --n)
{
int k = r.Next(n + 1);
Card temp = cards[n];
cards[n] = cards[k];
cards[k] = temp;
}
}
(Note that this method implements the Knuth-Fisher-Yates shuffle I've written about before)
Finally, we need a Draw() method, which returns a certain number of cards from the top of the deck. Given that our collection of cards is a List<>, we can use LINQ's Take() statement to give us the cards.
public List<Card> Draw(int count)
{
var drawnCards = Cards.Take(count).ToList();
//Remove the drawn cards from the draw pile
Cards.RemoveAll(x => drawnCards.Contains(x));
return drawnCards;
}
Ta-da! We've completed our CardDeck class, which means that we can move on to the next step: players!
Summary
In this post, we learned how to play UNO, saw my mad paint skillz put to good use, and modeled some cards. In the next post of this series, we will tackle the most complex part of this model: how the players behave.
Don't forget to check out the GitHub repository for this series!
Happy Coding!